Common projectile motion questions (not my work)

[http://zonalandeducation.com/mstm/physics/mechanics/curvedMotion/projectileMotion/generalSolution/generalSolution.html]

                                                                 

                                                                                               ↓

Original, or initial, conditions:

The original conditions are the size of the velocity and the angle above the horizontal with which the projectile is thrown.
General:

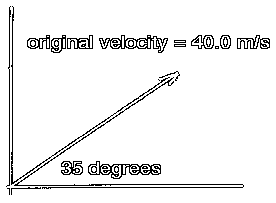
Original size of velocity: v_o
Original angle: theta

Example:

v_o = 40.0 m/s
theta = 35 degrees

Components of original velocity:

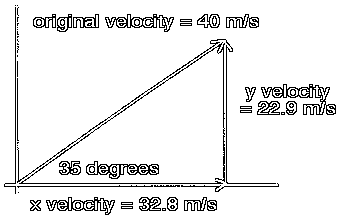
The usual first step in this investigation is to find the x and y components for the original velocity.
General:

X component of original velocity: v_ox = v_ocos(theta)
Y component of original velocity: v_oy = v_osin(theta)

Example:

In the x direction:

v_ox = v_ocos(theta)
v_ox = (40.0 m/s)(cos(35 degrees))
v_ox = (40.0)(0.8191)
v_ox = 32.76
v_ox = 32.8 m/s

In the y direction:

v_oy = v_osin(theta)
v_oy = (40.0 m/s)(sin(35 degrees))
v_oy = (40.0)(0.5735)
v_oy = 22.94
v_oy = 22.9 m/s

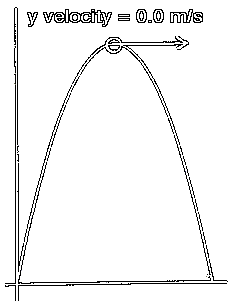
How much time passes until the projectile is at the top of its trajectory?

At the top of the trajectory the y, or upward, velocity of the projectile will be 0.0 m/s. The object is still moving at this moment, but its velocity is purely horizontal. At the top it is not moving up or down, only across.

Notice that the object is still in motion at the top of the trajectory; however, its velocity is completely horizontal. It has stopped going up and is about to begin going down. Therefore, its y velocity is 0.0 m/s.
We need to find out how much time passes from the time of the throw until the time when the y velocity of the projectile becomes 0.0 m/s. This y velocity at the top of the trajectory can be thought of as the final y velocity for the projectile for the portion of its flight that starts at the throw and ends at the top of the trajectory.
We will call this amount of time 'the half time of flight', since the projectile will spend one half of its time of flight rising to the top of its trajectory. It will spend the second half of its time of flight moving downward.
General:

We can use the following kinematics equation:

v_f = v_o + at

Subscript it for y:

v_fy = v_oy + a_yt

Solve it for t:

t = (v_fy - v_oy) / a_y

Plug in 0.0 m/s for v_fy:

t = (0.0 m/s - v_oy) / a_y

If the original y velocity and the y acceleration, i. e., the acceleration due to gravity, are plugged into the above equation, it will solve for the amount of time that passes from the moment of release to the moment when the projectile is at the top of its flight.

Example:

Start with:

t = (v_fy - v_oy) / a_y

Plug in 0.0 m/s for v_fy:

t = (0.0 m/s - v_oy) / a_y

Plug in values for v_oy and a_y:

t = (0.0 m/s - 22.9 m/s) / - 9.8 m/s²
t = -22.9 / -9.8
t = 2.33
t = 2.3 s

In this example 2.3s of time passes while the projectile is rising to the top of the trajectory.

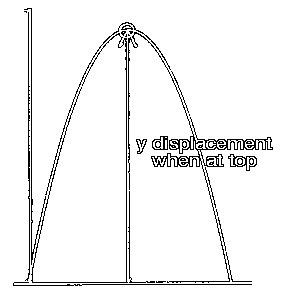
How high does the projectile rise?

Here you need to find the displacement in the y direction at the time when the projectile is at the top of its flight. We have just found the time at which the projectile is at the top of its flight. If we plug this time into a kinematics formula that will return the displacement, then we will know how high above ground the projectile is at when it is at the top of its trajectory.
General:

Here is the displacement formula:
d = v_ot + 0.5at²
We must think of this displacement in the y direction, so we will subscript this formula for y:
d_y = v_oyt + 0.5a_yt²
If now we plug in the half time of flight, which was found above, we will solve for the height of the trajectory, since the projectile is at its maximum height at this time.

Example:

Starting with:
d_y = v_oyt + 0.5a_yt²
Then plugging in known values:
d_y = (22.9 m/s)(2.33 s) + (0.5)(-9.8 m/s²)(2.33 s)²
d_y = 53.35 - 26.60
d_y = 26.75
d_y = 27 m

How much time passes until the projectile strikes the ground?

General:

With no air resistance, the projectile will spend an equal amount of time rising to the top of its projectile as it spends falling from the top to the ground. Since we have already found the half time of flight, we need only to double that value to get the total time of flight.

Example:

t = 2(2.33 s)
t = 4.66
t = 4.7 s
This is the total time of flight.

How far away does the projectile land from its starting point?

The distance from the starting point on the ground to the landing point on the ground is called the range of the trajectory. This range is a displacement in the x direction. It is governed by the x velocity of the projectile. This x velocity does not change during the flight of the projectile. That is, whatever is the value of the x velocity at the start of the trajectory will be the value of the x velocity throughout the flight of the projectile. The x velocity remains constant because there are no accelerations in the x direction. The only acceleration is in the y direction, and this is due to the vertical pull of gravity. Gravity does not pull horizontally. Therefore, the calculation for the range is simplified.
General:

Let us start with the general displacement formula:
d = v_ot + 0.5at²
Since we are working in the x direction, we should subscript this equation for x:
d_x = v_oxt + 0.5a_xt²
Now, since the acceleration in the x direction is 0.0 m/s², the second term in the above equation drops out, and we are left with:
d_x = v_oxt
The velocity in the x direction does not change. The projectile maintains its original x velocity throughout its entire flight. So, the original x velocity is the only x velocity the projectile will have. We could, therefore, think of the last equation as:
d_x = v_xt
If we plug in the original x velocity for v_x and the total time of flight for t, we will solve for the horizontal displacement, or range, of the trajectory.